
įor the images I thank my ex-professor Niloy Mitra as I found them in some notes I took for his lectures. If you are interested in the subject (and to add some reference to this post) an excellent read is: Discrete Differential-Geometry Operatorsįor Triangulated 2-Manifolds. If the edge has positions $p_1, p_2$ and normals $n_1, n_2$, then I estimated its curvature as:
Postview principal curvature skin#
Math.When I needed an estimate of mesh curvature for a skin shader, the algorithm I ended up settling on was this:įirst, I computed a scalar curvature for each edge in the mesh. Yau, S.T.: Harmonic functions on complete Riemannian manifolds. Wu, B.Y.: On hypersurfaces with two distinct principal curvatures in space forms. Wu, B.Y.: On hypersurfaces with two distinct principal curvatures in a hyperbolic space.
Postview principal curvature software#
For each participant’s original bone reconstructions, the general regions of interest for articulating surfaces of the subtalar joint (posterior and anteromedial facets) were isolated using values of 2nd principal of curvature calculated in the PostView software (v2.1.0, FEBio Software Suite, University of Utah, Salt Lake City, UT). Wu, B.Y.: On hypersurfaces with two distinct principal curvatures in Euclidean space. Subtalar Joint Coverage, Space and Congruency. 25 The joint center was defined as the center of the best-fit sphere to the lunate surface.

Wu, B.Y.: On hypersurfaces with two distinct principal curvatures in a unit sphere. The clockface was defined by computing the second principal curvature of the pelvis mesh using PostView software (Version 2.1 University of Utah) 14 to isolate the acetabular lunate surface and rim. Wei, G.: Rigidity theorem for hypersurfaces in a unit sphere. Wei, G.: Complete hypersurfaces with constant mean curvature in a unit sphere. Wang, Q.: Rigidity of Clifford minimal hypersurfaces. For this reason we did not combine them like in Gaussian curvature with k gaussian i k i 1 k i 2: (7) Each curvature are processed independently. Sousa Jr., L.A.M.: Rigidity theorems of Clifford torus. Principal curvatures histogram The key novelty of our approach is to preserve the data related to k i 1 and k i 2. Simons, J.: Minimal varieties in Riemannian manifolds. (v.2.0, University of Utah, Salt Lake City, UT, USA). Shu, S., Liu, S.: Hypersurfaces with two distinct principal curvatures in a real space form. models, the lunate surface and the head surface were selected using principal curvature in Postview. If at the umbilic, then has a local minimum and has a local maximum if.
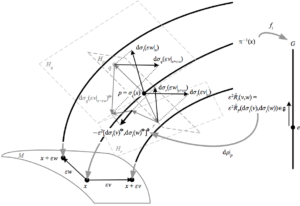
A best-fit cylindrical axis was calculated from these selections (Kapron et al., 2014). (Criterion for extrema of principal curvature functions at umbilics): If we assume that is at least smooth and at least one of the second order partial derivatives of does not vanish then: If at the umbilic, then has a local minimum and has a local maximum. I At a hyperbolic point, the Gaussian curvature is negative. Articulating (convex) surfaces of the trochlea and capitellum were also selected using 1st principal curvature. The points of a sphere are elliptic points. Shu, S., Han, A.Y.: Hypersurfaces with two distinct principal curvatures in a real space form. principal curvatures have the same sign, and therefore all curves passing through this point have their normal vectors pointing toward the same side of the tangent plane. Shiohama, K., Xu, H.: A general rigidity theorem for complete submanifolds. Perdomo, O.: Rigidity of minimal hypersurfaces of spheres with two principal curvatures. Peng, C.K., Terng, C.L.: Minimal hypersurfaces of spheres with constant scalar curvature. Otsuki, T.: Minimal hypersurface in a Riemannian manifold of constant curvature. Omori, H.: Isometric immersions of Riemannian manifolds. Alías, L.J., de Almeida, S.C., Brasil Jr., A.: Hypersurfaces with constant mean curvature and two principal curvatures in \(\mathbb\).


 0 kommentar(er)
0 kommentar(er)
